Question

If f(x)=x/2-3 and g(x)=3x^2+x-6, find (f+g)(x)

Answer 1

Hello!

The answer is:

`f(x)+g(x)=3x^(2) +(3x)/(2)-9`

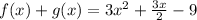
Why?

We are working with function addition, to add or subtract two o more functions, we need to follow the following form:

`(f+g)=f(x)+g(x)`

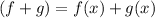
To simplify the expression, we need to work with the like terms, like terms are the terms that share the same variable and the same coefficient, for example:

`x+3x+x^(2)=x^(2) +4x`

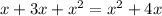
We were able to add only the first two terms since the third term does not share the exponent with the other two.

We are given the functions:

`f(x)=(x)/(2)-3\\\\g(x)=3x^(2)+x-6`

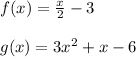
So, solving, we have:

`f(x)+g(x)=((x)/(2) -3)+(3x^(2) +x-6)\\\\f(x)+g(x)=3x^(2)+(x)/(2)+x-3-6\\\\f(x)+g(x)=3x^(2)+(x+2x)/(2)-9\\\\f(x)+g(x)=3x^(2) +(3x)/(2)-9`

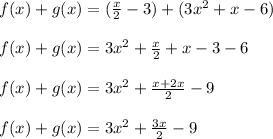
Hence, the answer is:

`f(x)+g(x)=3x^(2) +(3x)/(2)-9`

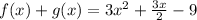
Have a nice day!