Hello!
The answer is:
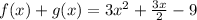
Why?
We are working with function addition, to add or subtract two o more functions, we need to follow the following form:
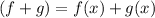
To simplify the expression, we need to work with the like terms, like terms are the terms that share the same variable and the same coefficient, for example:
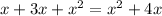
We were able to add only the first two terms since the third term does not share the exponent with the other two.
We are given the functions:
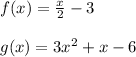
So, solving, we have:
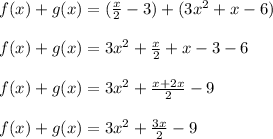
Hence, the answer is:
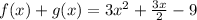
Have a nice day!