ANSWER
Domain:
All real numbers
Range:
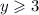
Step-by-step explanation
The given function is
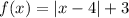
This is the function obtained by the shifting the base absolute value function to the right by 4 units and up by 3 units.
The vertex of this function is at:
(4,3)
The domain is all real numbers because there is no x-value that will make the function undefined.
The least y-value on this graph is 3.
The graph opens up forever.
The range is [3,∞) or y≥3