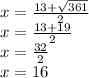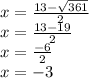Question

The answer of the problem

Answer 1

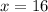`x=16` and
`x=-3`

Explanation:

A second-degree equation or quadratic equation of a variable is an equation that it has the general expression:

`ax^(2) +bx+c=0` with
`a\\eq 0`

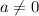
Where x is the variable, and a, b and c constants; a is the quadratic coefficient (other than 0), b the linear coefficient and c is the independent term. This polynomial can be interpreted by means of the graph of a quadratic function, that is, by a parabola. This graphical representation is useful, because the abscissas of the intersections or point of tangency of this graph, in the case of existing, with the X axis are the real roots of the equation. If the parabola does not cut the X axis the roots are complex numbers, they correspond to a negative discriminant.

Second degree equation solutions

For a quadratic equation with real or complex coefficients there are always two solutions, not necessarily different, called roots, which can be real or complex (if the coefficients are real and there are two non-real solutions, then they must be complex conjugates). General formula for obtaining roots:

`x=\frac{-b±\sqrt{b^(2) -4ac} }{2a}`

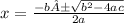
The discriminant serves to analyze the nature of the roots that can be real or complex.

Δ
`=b^(2) -4ac`

Solving the problem of the answer.

`x^(2) -13x-48=0` with a = 1, b = -13, and c = -48

Substituting the values in the general formula for a quadratic equation.

`x=\frac{-(-13)±\sqrt{(-13)^(2) -4(1)(-48)} }{2(1)}`

`x=(13±√(169+192) )/(2)`

`x=(13±√(361) )/(2)`

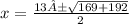
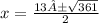
Then, we obtain the roots:

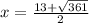`x=(13+√(361) )/(2)` and
`x=(13-√(361) )/(2)`

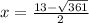
Solving the roots:

`x=(13+√(361) )/(2)\\x=(13+19)/(2)\\x=(32)/(2)\\x=16`

`x=(13-√(361) )/(2)\\x=(13-19)/(2)\\x=(-6)/(2)\\x=-3`