Question

The value of a $3000 computer decreases about 30% each year. write a function for the computers value V(t)

How much will the computer be worth in 4 years?​

Answer 1

A = $3000(0.70)^t

Explanation:

100% - 30% = 70%. Thus, the common ratio in this exponential function is 0.70.

Use a formula with the form of the compound amount formula:

A = P(1 + r)^t, where r is the common ratio as a decimal fraction and t is the number of years.

Here, A = $3000(1 - 0.30)^t, or A = $3000(0.70)^t

Answer 2

Function for given situation is :
`V(t)=3000(0.70)^t`

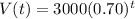
Value of computer after 4 years = $720.3.

Explanation:

Given that the value of a $3000 computer decreases about 30% each year. Now we need to write a function for the computers value V(t). then we need to find about how much will the computer be worth in 4 years.

It clearly says that value decreases so that means function represents decay.

For decay we use formula:

`A=P(1-r)^t`

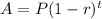
where P=initial value = $3000,

r= rate of decrease =30% = 0.30

t= number of years

A=V(t) = future value

so the required function is
`V(t)=3000(1-0.30)^t`

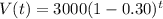
or
`V(t)=3000(0.70)^t`

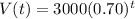
Now plug t=4 years to get the value of computer after 4 years.

`V(4)=3000(0.70)^4`

`V(4)=720.3`

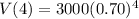
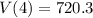
Hence final answer is $720.3.