Answer:
Sum of the interior angles = (n-2) x 180°
where
n is the number of sides of the polygon
Step-by-step explanation:
The formula for the sum of the interior angles of a polygon is:
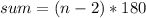
where
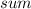 is the sum of the interior angle of the polygon
is the sum of the interior angle of the polygon
 is the number of polygons
is the number of polygons
Let's check the formula using an example:
We want to find the sum of the interior angles of a square, we know that a square has 4 sides, so
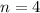 .
.
Replacing values
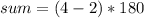
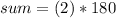
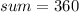
We can apply the same procedure to any convex polygon with n sides.