Question

The ratio of the number of men to the number of women on a bus was 2:3 at a bus stop. 4 women got off and the ratio became 4:5. 1 How many men were on the bus? b. How many women were on the bus in the end?

Answer 1

At the beginning

16 men and 24 women

In the end

16 men and 20 women

Explanation:

Call x the number of men on the bus and call y the number of women on the bus.

We know that the initial ratio between men and women is 2: 3

And the final ratio is 4: 5

So

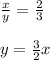`(x)/(y)=(2)/(3)\\\\y = (3)/(2)x` (1)

After the 4 women are down, the proportion is:

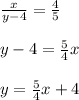`(x)/(y-4)=(4)/(5)\\\\y-4 = (5)/(4)x\\\\y= (5)/(4)x +4` (2)

Substitute the value of y in the first equation and solve for x

`(5)/(4)x +4=(3)/(2)x\\\\-(1)/(4)x=-4\\\\x=16\ men`

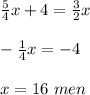
Now solve for y.

`y = (3)/(2)(16)\\\\y=24\ women`

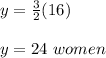
Then at the end there were 20 women (because 4 women got off the bus)

Answer 2

16 men

20 women

Explanation:

We are given that the ratio of the number of men to the number of women on a bus was 2:3 at a bus stop.

So assuming x to be the number of persons (male or female), we can write it as:

`\frac {2x}{3x}`

When 4 women got off the bus, the ratio changed to 4:5.

`\frac {2x} {3x-4} = \frac {4} {5}`

Solving it to find x:

`5(2x)=4(3x-4)`

`10x=12x-16`

`2x=16`

`x=8`

So, number of men on the bus =
`2(8)` = 16

and number of women on the bus at the end =
`3(8)-4 = 24-4` = 20