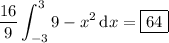Question

Find the volume V of the described solid S. The base of S is an elliptical region with boundary curve 16x2 + 9y2 = 144. Cross-sections perpendicular to the x-axis are isosceles right triangles with hypotenuse in the base.

Answer 1

In the
`x`-
`y` plane, the base has equation(s)

`16x^2+9y^2=144\implies y=\pm\frac43√(9-x^2)`

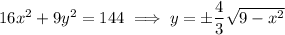
which is to say, the distance (parallel to the
`y`-axis) between the top and the bottom of the ellipse is

`\frac43√(9-x^2)-\left(-\frac43√(9-x^2)\right)=\frac83√(9-x^2)`

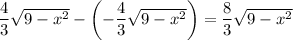
so that at any given
`x`, the cross-section has a hypotenuse whose length is
`\frac83√(9-x^2)`.

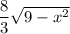The cross-section is an isosceles right triangle, which means the legs occur with the hypotenuse in a ratio of 1 to
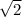`\sqrt2`, so that the legs have length
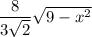`\frac8{3\sqrt2}√(9-x^2)`. Then the area of each cross-section is

`\frac12\left(\frac8{3\sqrt2}√(9-x^2)\right)\left(\frac8{3\sqrt2}√(9-x^2)\right)=\frac{16}9(9-x^2)`

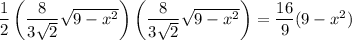
Then the volume of this solid is

`\displaystyle\frac{16}9\int_(-3)^39-x^2\,\mathrm dx=\boxed{64}`