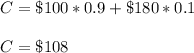Question

Two different antibiotics can be used to treat an infection. Treatment with antibiotic 1 is known to be successful 80% of the time. This treatment costs $80. Antibiotic 2 is successful 90% of the time and costs $100. The two treatment plans are: Plan A: Treat with antibiotic 1. If not effective, treat with antibiotic 2. Plan B: Treat with antibiotic 2. If not effective, treat with antibiotic 1. Based on the data provided, what is the expected cost per patient under plan B?

A. $100
B. $80
C. $180
D. $108

Answer 1

Answer: Option D

D. $108

Explanation:

We must calculate the expected cost per patient to use treatment method B.

The expected cost for a discrete random variable x is:

`C = \sum x_i * P (x_i)`

Where
`x_i` is the cost associated with the probability
`P(x_i)`

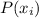
In this case, the random variable x is represented by the cost of each treatment.

For treatment B there is a possibility that antibiotic 2 works, in that case the cost x would be $ 100 and
`P (x) = 0.9`

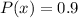
There is also the possibility that it does not work, in this case the cost x would be $180 and the probability
`P (x) = 0.10`

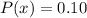
The expected cost is:

`C =\$100*0.9 + \$180*0.1\\\\C = \$108`