Question

The asymptote of the function f(x) = 3^x + 1 – 2 is ______. Its y-intercept is _____.

x+1 is the exponent.

Answer 1

Y-intercept;

(0, 1)

Asymptote;

Horizontal asymptote: y = -2

Explanation:

We have been given the following exponential function;

`f(x) = 3^(x+1)-2`

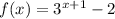
The y-intercept of a function is the point where the graph of the function intersects the y-axis. At this point, the value of x is usually 0. Therefore, to establish the y-intercept of the given function we substitute x with 0 in the given equation and simplify;

`y=3^(0+1)-2\\ \\y=3-2=1`

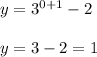
The y-intercept of the given function is thus (0, 1).

Exponential function of the form;

`f(x)=c.n^(ax+b)+k`

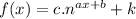
has a horizontal asymptote y = k. In the function given, k = -2 implying that

y = -2 is a horizontal asymptote of the given exponential function