Answer:
Y-intercept;
(0, 1)
Asymptote;
Horizontal asymptote: y = -2
Explanation:
We have been given the following exponential function;
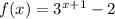
The y-intercept of a function is the point where the graph of the function intersects the y-axis. At this point, the value of x is usually 0. Therefore, to establish the y-intercept of the given function we substitute x with 0 in the given equation and simplify;
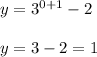
The y-intercept of the given function is thus (0, 1).
Exponential function of the form;
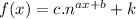
has a horizontal asymptote y = k. In the function given, k = -2 implying that
y = -2 is a horizontal asymptote of the given exponential function