Question

4.5 cm3 of water is boiled at atmospheric pressure to become 4048.3 cm3 of steam, also at atmospheric pressure. Calculate the work done by the gas during this process. The latent heat of vaporization of water is 2.26 × 106 J/kg . Answer in units of J. 006 (part 2 of 3) 10.0 points Find the amount of heat added to the water to accomplish this process. Answer in units of J.

Answer 1

1. 408.4 J

The work done by a gas is given by:

`W=p\Delta V`

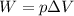
where

p is the gas pressure

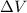`\Delta V` is the change in volume of the gas

In this problem,

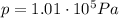`p=1.01\cdot 10^5 Pa` (atmospheric pressure)

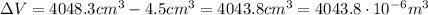`\Delta V=4048.3 cm^3 - 4.5 cm^3 =4043.8 cm^3 = 4043.8 \cdot 10^(-6)m^3` is the change in volume

So, the work done is

`W=(1.01\cdot 10^5 Pa)(4043.8 \cdot 10^(-6)m^3)=408.4 J`

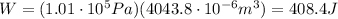
2. 10170 J

The amount of heat added to the water to completely boil it is equal to the latent heat of vaporization:

`Q = m \lambda_v`

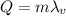
where

m is the mass of the water

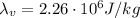`\lambda_v = 2.26\cdot 10^6 J/kg` is the specific latent heat of vaporization

The initial volume of water is

`V_i = 4.5 cm^3 = 4.5\cdot 10^(-6)m^3`

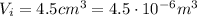
and the water density is

`\rho = 1000 kg/m^3`

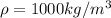
So the water mass is

`m=\rho V_i = (1000 kg/m^3)(4.5\cdot 10^(-6)m^3)=4.5\cdot 10^(-3)kg`

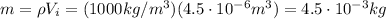
So, the amount of heat added to the water is

`Q=(4.5\cdot 10^(-3)kg)(2.26\cdot 10^6 J/kg)=10,170 J`