Question

"Find four numbers proportional to the numbers 2, 4, 5, and 6 if the difference between the sum of the two last numbers and the sum of the first two numbers is equal to 4.8."

Answer 1

`\boxed{\text{1.92, 3.84, 4.80, and 5.76}}`

Explanation:

The numbers must be in the ratio 2:4:5:6.

Let's call them 2x, 4x, 5x, and 6x. Then

5x + 6x = 11x = sum of last two numbers

2x + 4x = 6x = sum of first two numbers

According to the condition,

11x – 6x = 4.8

5x = 4.8

x = 0.96

2x = 1.92; 4x = 3.84; 5x = 4.80; 6x = 5.76

The numbers are
`\boxed{\textbf{1.92, 3.84, 4.80, and 5.76}}`

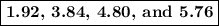
Check:

(4.80 + 5.76) – (1.92 + 3.84) = 4.8

10.56 – 5.76 = 4.8

4.8 = 4.8

OK.

Answer 2

1.92, 3.84, 4.8, 5.76

Explanation:

In the given set, the sum of the last two numbers is 5+6 = 11; the sum of the first two numbers is 2+4 = 6. The difference between these sums is 11-6 = 5.

You want to scale all the numbers by a factor of 4.8/5 = 0.96 so that the difference computed the same way is 4.8 instead of 5.

Then the numbers are ...

0.96{2, 4, 5, 6} = {1.92, 3.84, 4.8, 5.76}