We need two things to write the recursive formula
- The first term,

- The common difference,
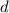
 is the first value of this sequence. For this set of values,
is the first value of this sequence. For this set of values,
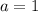 , since
, since
 appears first.
appears first.
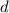 , the common difference, is
, the common difference, is
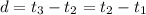 . Basically it's just the the higher term minus the previous terms. To solve for
. Basically it's just the the higher term minus the previous terms. To solve for
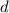 ,
,
So regardless of what terms you choose, the common difference will be the same. Now the general formula for a recursive function is
where
 is the
is the
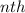 term. Let's substitute for
term. Let's substitute for
 and
and
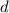 in this formula.
in this formula.

So the recursive formula is
