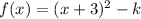Question

What is the quadratic function f(x)=x^2+6x-2 In vertex form?

A:f(x)=(x-3)^2+7
B:f(x)=(x+3)^2+7
C:f(x)=(x-3)^2-11
D:f(x)=(x+3)^2-11

Answer 1

The correct answer option is D. f(x) = (x + 3)² - 11.

Explanation:

We know that the standard form of a quadratic function is given by:

y = ax² + bx + c

The vertex form of a parabola is given by

y = a(x - h)² + k

where (h, k) is the vertex of the parabola.

h = -b / 2a and k = f(h)

In the given equation f(x) = x² + 6x - 2

a = 1, b = 6 and c = -2

Finding h:

h = -6 / (2 × 1)

h = -6/2

h = -3

Finding k:

k = 1(-3)² + 6(-3) + 3

k = 9 - 18 - 2

k = -11

Therefore, the given quadratic function in vertex form: f(x) = (x + 3)² - 11

Answer 2

Answer: Option D

`f(x)=(x+3)^2 -k`

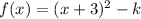
Explanation:

For a quadratic function of the form

`ax ^ 2 + bx + c`

The x coordinate of the vertice is:

`x =-(b)/(2a)`

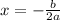
In this case the function is:

`f(x)=x^2+6x-2\\\\`

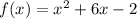
So

`a=1\\b=6\\c=-2`

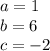
The x coordinate of the vertice is:

`x=-(6)/(2*1)\\\\x=-3`

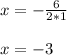
The y coordinate of the vertice is:

`f(-3) = (-3)^2 +6(-3) -2\\\\f(-3)=-11`

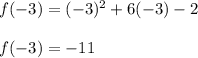
The vertice is: (-3, -11)

The form e vertice for a quadratic equation is:

`f(x)=(x-h)^2 +k`

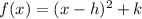
Where

the x coordinate of the vertice is h and the y coordinate of the vertice is k.

Then h=-3 and k =-11

Finally the equation
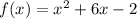`f(x)=x^2+6x-2\\\\` in vertex form is:

`f(x)=(x+3)^2 -k`