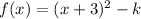Answer: Option D
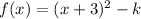
Explanation:
For a quadratic function of the form
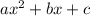
The x coordinate of the vertice is:
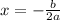
In this case the function is:
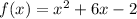
So
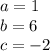
The x coordinate of the vertice is:
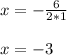
The y coordinate of the vertice is:
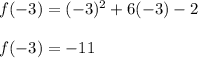
The vertice is: (-3, -11)
The form e vertice for a quadratic equation is:
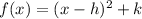
Where
the x coordinate of the vertice is h and the y coordinate of the vertice is k.
Then h=-3 and k =-11
Finally the equation
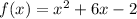 in vertex form is:
in vertex form is: