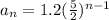Answer:
The formula is:
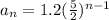
Explanation:
The geometric sequences are those in which the division between the terms
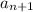 and
and
 of the sequence are equal to a constant common reason called "r"
of the sequence are equal to a constant common reason called "r"
The geometrics secencias have the following form:
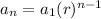
Where
 is the first term of the sequence
is the first term of the sequence
In this sequence we have the following terms
1.2, 3, 7.5, 18.75
Then notice that:
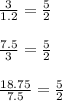
Then:
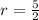 and
and
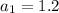
Finally the formula is: