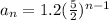Question

1.2, 3, 7.5, 18.75, ...

Which formula can be used to describe the sequence?

Answer 1

Answer: "f(x) = 1.2(2.5)x-1"

Explanation:

Answer 2

The formula is:

`a_n=1.2((5)/(2))^(n-1)`

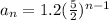
Explanation:

The geometric sequences are those in which the division between the terms
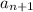`a_(n + 1)` and
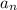`a_n` of the sequence are equal to a constant common reason called "r"

The geometrics secencias have the following form:

`a_n=a_1(r)^(n-1)`

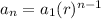
Where
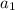`a_1` is the first term of the sequence

In this sequence we have the following terms

1.2, 3, 7.5, 18.75

Then notice that:

`(3)/(1.2)=(5)/(2)\\\\(7.5)/(3)=(5)/(2)\\\\(18.75)/(7.5)=(5)/(2)`

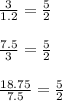
Then:

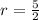`r=(5)/(2)` and
`a_1=1.2`

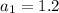
Finally the formula is:

`a_n=1.2((5)/(2))^(n-1)`