Answer:
The answer is the 1st
![\frac{\left[\begin{array}{cc}16&3\\8&1\end{array}\right]}{-8}=1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7w0f81ste49deb9qpogyfd2ditu3pbxcdj.png)
Explanation:
Lets revise the Cramer's rule
- If the system of equation is ax + by = c and dx + ey = f
- A is the matrix represent this system of equation
- The first column has the coefficients of x, and
the second column has the coefficients of y
∴ A =
![\left[\begin{array}{cc}a&b\\d&e\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lgxyqrhjrb1tc0yifq26dyoornr016x0qf.png)
- Ax means replace the column of x by the answers of the equation
∴ Ax =
![\left[\begin{array}{ccc}c&b\\f&e\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kbalx3njx9s7ghliwvg98fufhto5011qbv.png)
- Ay means replace the column of y by the answers of the equation
∴ Ay =
![\left[\begin{array}{ccc}a&c\\d&f\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/malxw3i4li4qtods30sewwdberyekd8owp.png)
- x = Dx/D, where Dx is the determinant of Ax and D is the determinant
of A
- The determinant of A = ae - bd
- The determinant of Ax = ce - bf
* Now lets solve the problem
∵ x + 3y = 16 and 3x + y = 8
∴ A =
![\left[\begin{array}{cc}1&3\\3&1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/drqznro1osqorur9nre7z07zrb7bfm5vlq.png)
- Replace the column of x by the answer to get Ax
∴ Ax =
![\left[\begin{array}{cc}16&3\\8&1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/gd528ggtm4ays4w4lnt86aj518q896rawi.png)
∵
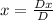
∵ Dx =
![\left[\begin{array}{cc}16&3\\8&1\end{array}\right]=(16)(1)-(3)(8)=16-24=-8](https://img.qammunity.org/2020/formulas/mathematics/middle-school/b5gqgz89zihlkzdo5vizo31b38bzq8k48n.png)
∵ D =
![\left[\begin{array}{cc}1&3\\3&1\end{array}\right]=(1)(1)-(3)(3)=1-9=-8](https://img.qammunity.org/2020/formulas/mathematics/middle-school/27s4n839el8q0obzawjw2p535p4bgv7sjm.png)
∴ x =
![\frac{\left[\begin{array}{cc}16&3\\8&1\end{array}\right]}{-8}=(-8)/(-8)=1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vw9w98z87foo5oaene7llcld5dt8d32gsj.png)
* x =
![\frac{\left[\begin{array}{cc}16&3\\8&1\end{array}\right]}{-8}=1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7w0f81ste49deb9qpogyfd2ditu3pbxcdj.png)