Question

Using Cramer’s Rule, what is the value of x in the system of linear equations below?

Answer 1

The answer is the 1st
`\frac{\left[\begin{array}{cc}16&3\\8&1\end{array}\right]}{-8}=1`

Explanation:

Lets revise the Cramer's rule

- If the system of equation is ax + by = c and dx + ey = f

- A is the matrix represent this system of equation

- The first column has the coefficients of x, and

the second column has the coefficients of y

∴ A =
`\left[\begin{array}{cc}a&b\\d&e\end{array}\right]`

- Ax means replace the column of x by the answers of the equation

∴ Ax =
`\left[\begin{array}{ccc}c&b\\f&e\end{array}\right]`

- Ay means replace the column of y by the answers of the equation

∴ Ay =
`\left[\begin{array}{ccc}a&c\\d&f\end{array}\right]`

- x = Dx/D, where Dx is the determinant of Ax and D is the determinant

of A

- The determinant of A = ae - bd

- The determinant of Ax = ce - bf

* Now lets solve the problem

∵ x + 3y = 16 and 3x + y = 8

∴ A =
`\left[\begin{array}{cc}1&3\\3&1\end{array}\right]`

- Replace the column of x by the answer to get Ax

∴ Ax =
`\left[\begin{array}{cc}16&3\\8&1\end{array}\right]`

∵
`x=(Dx)/(D)`

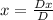
∵ Dx =
`\left[\begin{array}{cc}16&3\\8&1\end{array}\right]=(16)(1)-(3)(8)=16-24=-8`

∵ D =
`\left[\begin{array}{cc}1&3\\3&1\end{array}\right]=(1)(1)-(3)(3)=1-9=-8`

∴ x =
`\frac{\left[\begin{array}{cc}16&3\\8&1\end{array}\right]}{-8}=(-8)/(-8)=1`

* x =
`\frac{\left[\begin{array}{cc}16&3\\8&1\end{array}\right]}{-8}=1`