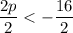Answer:
p > 5 and p <-8
Explanation:
To solve this, you first need to isolate p.
First add 6 on both sides of the equation:
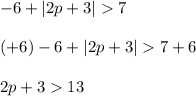
Then subtract 3 from both sides of the equation.
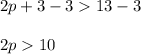
The divide both sides by 2.
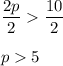
Another solution is possible because of the absolute value.
If
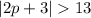
Then
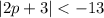
Thus we can solve the second solution:
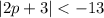
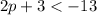
Isolate P again by subtracting both sides by 3
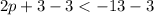
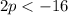
Then divide both sides by 2: