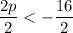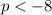Question

What is the solution to the inequality

Answer 1

p > 5, p < -8

Explanation:

We are given the following inequality and we are to find its solution:

`-6+|2p+3|>7`

Adding 6 to both sides to get:

`-6+6+|2p+3|>7+6`

`|2p+3|>13`

We know the absolute rule that
`\mathrm{If}\:|u|\:>\:a,\:a>0\:\mathrm{then}\:u\:<\:-a\:\quad \mathrm{or}\quad \:u\:>\:a`.

So
`2p+3>13` or
`2p+3<-13`

`2 p > 1 3 - 3`,
`2 p < - 1 3 - 3`

`2 p > 1 0`,
`2 p < - 1 6`

`p>(10)/(2)`,
`p<(-16)/(2)`

p > 5, p < -8

Answer 2

p > 5 and p <-8

Explanation:

To solve this, you first need to isolate p.

First add 6 on both sides of the equation:

`-6 + |2p+3| >7\\\\(+6) -6 + |2p+3| >7 +6\\\\2p + 3 > 13`

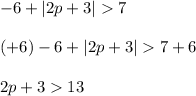
Then subtract 3 from both sides of the equation.

`2p+3-3>13-3\\\\2p > 10\\`

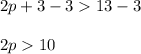
The divide both sides by 2.

`(2p)/(2)>(10)/(2)\\\\p>5`

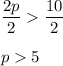
Another solution is possible because of the absolute value.

If
`|2p+3|>13`

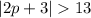
Then
`|2p+3|<-13`

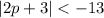
Thus we can solve the second solution:

`|2p+3|<-13`

`2p+3<-13`

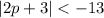
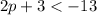
Isolate P again by subtracting both sides by 3

`2p+3-3<-13-3`

`2p<-16`

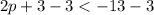
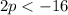
Then divide both sides by 2:

`(2p)/(2)<-(16)/(2)`

`p<-8`