A)
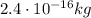
The radius of the oil droplet is half of its diameter:
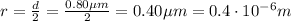
Assuming the droplet is spherical, its volume is given by
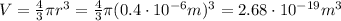
The density of the droplet is
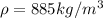
Therefore, the mass of the droplet is equal to the product between volume and density:
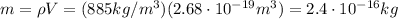
B)
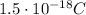
The potential difference across the electrodes is
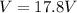
and the distance between the plates is

So the electric field between the electrodes is
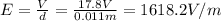
The droplet hangs motionless between the electrodes if the electric force on it is equal to the weight of the droplet:
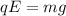
So, from this equation, we can find the charge of the droplet:
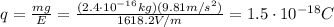
C) Surplus of 9 electrons
The droplet is hanging near the upper electrode, which is positive: since unlike charges attract each other, the droplet must be negatively charged. So the real charge on the droplet is
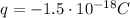
we can think this charge has made of N excess electrons, so the net charge is given by
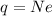
where
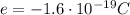 is the charge of each electron
is the charge of each electron
Re-arranging the equation for N, we find:
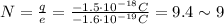
so, a surplus of 9 electrons.