Question

A 0.80-μm-diameter oil droplet is observed between two parallel electrodes spaced 11 mm apart. The droplet hangs motionless if the upper electrode is 17.8 V more positive than the lower electrode. The density of the oil is 885kg/m3. Part A What is the droplet's mass? Express your answer to two significant figures and include the appropriate units. m m = nothing nothing Request Answer Part B What is the droplet's charge? Express your answer to two significant figures and include the appropriate units. q q = nothing nothing Request Answer Part C Does the droplet have a surplus or a deficit of electrons? How many? Does the droplet have a surplus or a deficit of electrons? How many? deficit 9 electrons surplus 9 electrons surplus 16 electrons deficit 7 electrons

Answer 1

A)
`2.4\cdot 10^(-16)kg`

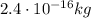
The radius of the oil droplet is half of its diameter:

`r=(d)/(2)=(0.80 \mu m)/(2)=0.40 \mu m = 0.4\cdot 10^(-6)m`

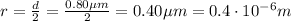
Assuming the droplet is spherical, its volume is given by

`V=(4)/(3)\pi r^3 = (4)/(3)\pi (0.4\cdot 10^(-6) m)^3=2.68\cdot 10^(-19) m^3`

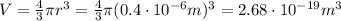
The density of the droplet is

`\rho=885 kg/m^3`

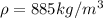
Therefore, the mass of the droplet is equal to the product between volume and density:

`m=\rho V=(885 kg/m^3)(2.68\cdot 10^(-19) m^3)=2.4\cdot 10^(-16)kg`

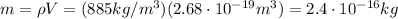
B)
`1.5\cdot 10^(-18)C`

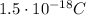
The potential difference across the electrodes is

`V=17.8 V`

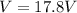
and the distance between the plates is

`d=11 mm=0.011 m`

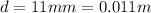
So the electric field between the electrodes is

`E=(V)/(d)=(17.8 V)/(0.011 m)=1618.2 V/m`

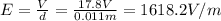
The droplet hangs motionless between the electrodes if the electric force on it is equal to the weight of the droplet:

`qE=mg`

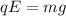
So, from this equation, we can find the charge of the droplet:

`q=(mg)/(E)=((2.4\cdot 10^(-16)kg)(9.81 m/s^2))/(1618.2 V/m)=1.5\cdot 10^(-18)C`

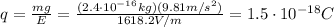
C) Surplus of 9 electrons

The droplet is hanging near the upper electrode, which is positive: since unlike charges attract each other, the droplet must be negatively charged. So the real charge on the droplet is

`q=-1.5\cdot 10^(-18)C`

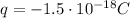
we can think this charge has made of N excess electrons, so the net charge is given by

`q=Ne`

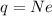
where

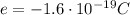`e=-1.6\cdot 10^(-19)C` is the charge of each electron

Re-arranging the equation for N, we find:

`N=(q)/(e)=(-1.5\cdot 10^(-18)C)/(-1.6\cdot 10^(-19)C)=9.4 \sim 9`

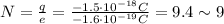
so, a surplus of 9 electrons.