Question

Let a and b be rational numbers. Then by definition

a = m/n and b = p/p where m, n, p, and q are integers
xy=m/n × p/q
ng
so xy is the quotient of two integers.
This proof shows that the product of two rational numbers is........
a. an integer
b. irrational
c. rational
d. a whole number ​

Answer 1

the product of two rational numbers is a rational number!

Explanation:

Answer 2

The product of two rational numbers is a rational number

Explanation:

I'll quickly recap the proof: a rational number is, by definition, the ratio between two integers. So, there exists four integers m,n,p,q such that

`a=(m)/(n),\quad b=(p)/(q)`

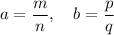
If we multiply the fractions, we have

`ab = (mp)/(nq)`

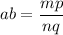
Now, mp and nq are multiplication of integers, and thus they are integers themselves. So, ab is also a ratio between integer, and thus rational.