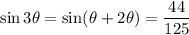is in quadrant I, so
is in quadrant I, so
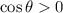 .
.
 is in quadrant II, so
is in quadrant II, so
 .
.
Recall that for any angle
 ,
,

Then with the conditions determined above, we get
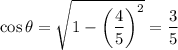
and

Now recall the compound angle formulas:
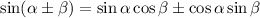
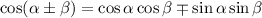
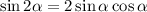
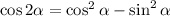
as well as the definition of tangent:
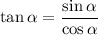
Then
1.
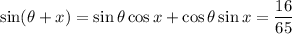
2.
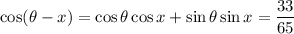
3.

4.
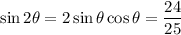
5.
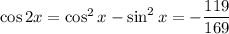
6.

7. A bit more work required here. Recall the half-angle identities:
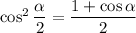
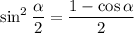
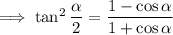
Because
 is in quadrant II, we know that
is in quadrant II, we know that
 is in quadrant I. Specifically, we know
is in quadrant I. Specifically, we know
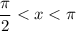 , so
, so
 . In this quadrant, we have
. In this quadrant, we have
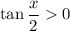 , so
, so
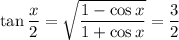
8.