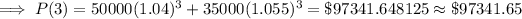Answer: The function would be,
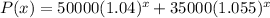
The approximate total profit after 4 years is $ 97341.65.
Explanation:
Given,
For branch A,
First year profit = $ 50,000,
And, the profit increased by 4% every year.
Thus, the profit of branch A after x years,
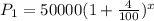
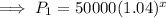
Also, for branch B,
First year profit = $ 35,000,
And, the profit increased by 5.5% every year.
Thus, the profit of branch B after x years,
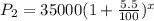
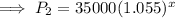
Hence, the total profit,
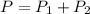
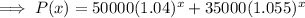
Which is the required function.
After 4 years, x = 3,
Therefore, the total profit after 4 years would be,