Answer:
x= 4-7i x= 4+ 7i
Explanation:
step 1 : make equation = 0
 - 8x + 65 = 0
- 8x + 65 = 0
step 2 : solve for x [ using the quadratic equation]
ie : x = -b ±
 / 2a
/ 2a
so it will look like this
x= -(-8) ±
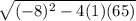 /2(1)
/2(1)
when you simplify you wont be able to root the -196 so you will have to separate the roots
x = 8 ±(
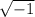 )(
)(
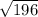 ) / 2
) / 2
now there is a rule for negative roots whereby
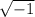 is equivalent to i so now you will change
is equivalent to i so now you will change
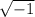 into i
into i
Simplify
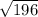
which will give you 14
now place all the new values into the formula
8 ± 14i /2
you can then further simplify to
4 ± 7i
step 3 : separate
this will give you the final answer of
x= 4 + 7i x= 4- 7i