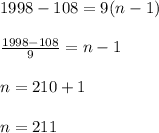Answer: First Option
The number of multiples of 9 is 211
Explanation:
Note that the first multiplo of 9 between 100 and 2000 is number 108. The last multiple of 9 is 1998.
If we use the arithmetic sequence to perform the calculation
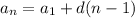
So the first term
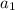 is:
is:
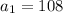
The last term
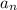 is
is
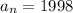
The common difference is
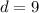
Thus
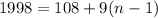
We solve the equation for n and obtain the number of multiples of 9.