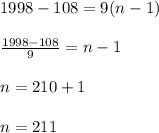Question

How many multiples of 9 are there between 100 and 2,000?

Hint: an = a1 + d (n − 1), where a1 is the first term and d is the common difference.


211


212


196


210

Answer 1

196.00000000000000000000000

Answer 2

Answer: First Option

The number of multiples of 9 is 211

Explanation:

Note that the first multiplo of 9 between 100 and 2000 is number 108. The last multiple of 9 is 1998.

If we use the arithmetic sequence to perform the calculation

`a_n = a_1 + d(n - 1)`

So the first term
`a_1` is:

`a_1 = 108`

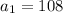
The last term
`a_n` is

`a_n = 1998`

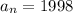
The common difference is

`d = 9`

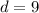
Thus

`1998 = 108 + 9(n-1)`

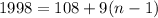
We solve the equation for n and obtain the number of multiples of 9.

`1998-108 = 9(n-1)\\\\(1998-108)/(9)=n-1\\\\n = 210 +1\\\\n = 211`