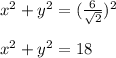Question

Write the equation in standard form of the circle whose center is at (0, 0) and that is tangent to x + y = 6

Answer 1

`x^2 + y^2 =18`

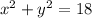
Explanation:

The standard equation of a circumference has the following formula.

`(x-h) ^ 2 + (y-k) ^ 2 = r ^ 2`

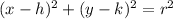
Where the point (h, k) is the center of the circle and r is the radius.

If in this case we know that the circle has center at point (0,0), then its equation will have the following form

`x ^ 2 + y ^ 2 = r ^ 2`

The radius of the circumference will be the distance from the center of the circumference to the point where the circumference is tangent to the line
`Ax + Bx + C = 0`

The radio is:

`r=(|Ah + Bk +C|)/(√(A^2+B^2))`

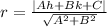
In this case, the line is

`x + y = 6`

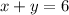
And the center of the circumference is (0, 0)

So

`A = 1\\B = 1\\C = -6\\h = 0\\k = 0`

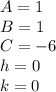
The radio is:

`r=(|1*0 + 1*0 -6|)/(√(1^2+1^2))\\\\r=(|-6|)/(√(1^2+1^2))\\\\r=(6)/(√(2))`

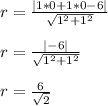
Finally the equation of the circumference is:

`x^2 + y^2 =((6)/(√(2)))^2\\\\x^2 + y^2 =18`