Answer:
Option (A) and (D) are not trigonometric identities.
Explanation:
Option (A ) tan²x + sec²x = 1
Since
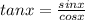 and
and
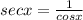
put these in left hand side of tan²x + sec²x = 1
 +
+
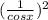
 +
+

Take L.C.M of above expression,
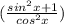
since, sin²x = 1 - cos²x
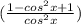
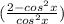
we are not getting 1
so, this is not a trigonometric identity.
Option (A) is correct option
Option (B) sin²x + cos²x = 1
This is an trigonometric identity
Option (C) sec²x - tan²x = 1
Divide the trigonometric identity sin²x + cos²x = 1 both the sides by cos²x so, we get

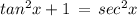
subtract both the sides by tan²x in above expression
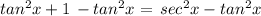
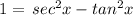
Hence, this is the trigonometric identity.
Option (D) sec²x + cosec²x = 1
Since
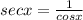 and
and
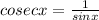
put these in left hand side of sec²x + cosec²x = 1
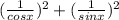
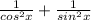
we are not getting 1
so, this is not a trigonometric identity.
Option (D) is correct option.
Hence, Option (A) and (D) are not trigonometric identities.