Question

Which of the following are not trigonometric identities? Check all that apply. A. tan^2x+sec^2x=1. B. sin^2x+cos^2x=1. C. sec^2x-tan^2x=1. D. sec^2x+csc^2x=1.

Answer 1

a

Explanation:

Answer 2

Option (A) and (D) are not trigonometric identities.

Explanation:

Option (A ) tan²x + sec²x = 1

Since
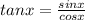`tanx =(sinx)/(cosx)` and
`secx =(1)/(cosx)`

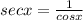
put these in left hand side of tan²x + sec²x = 1

`((sinx)/(cosx))^(2)` +
`((1)/(cosx))^(2)`

`((sin^(2)x)/(cos^(2)x))` +
`((1)/(cos^(2)x))`

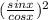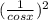
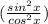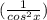
Take L.C.M of above expression,

`((sin^(2)x + 1)/(cos^(2)x))`

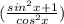
since, sin²x = 1 - cos²x

`((1-cos^(2)x+1)/(cos^(2)x))`

`((2-cos^(2)x)/(cos^(2)x))`

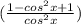
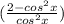
we are not getting 1

so, this is not a trigonometric identity.

Option (A) is correct option

Option (B) sin²x + cos²x = 1

This is an trigonometric identity

Option (C) sec²x - tan²x = 1

Divide the trigonometric identity sin²x + cos²x = 1 both the sides by cos²x so, we get

`(sin^(2)x)/(cos^(2)x)+(cos^(2)x)/(cos^(2)x)\,=\,(1)/(cos^(2)x)`

`tan^(2)x}+1\,=\,sec^(2)x}`

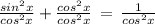
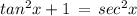
subtract both the sides by tan²x in above expression

`tan^(2)x}+1\,-tan^(2)x=\,sec^(2)x-tan^(2)x`

`1=\,sec^(2)x}-tan^(2)x`

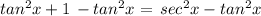
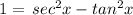
Hence, this is the trigonometric identity.

Option (D) sec²x + cosec²x = 1

Since
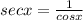`secx =(1)/(cosx)` and
`cosecx =(1)/(sinx)`

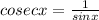
put these in left hand side of sec²x + cosec²x = 1

`((1)/(cosx))^(2)+((1)/(sinx))^(2)`

`(1)/(cos^(2)x)+(1)/(sin^(2)x)`

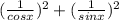
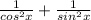
we are not getting 1

so, this is not a trigonometric identity.

Option (D) is correct option.

Hence, Option (A) and (D) are not trigonometric identities.