Answer:
The discriminant is equal to −16, which means the equation has no real number solutions.
Explanation:

we have to find the number of real number solutions the equation has.
The equation is
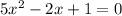

a=5, b=-2, c=1
To find number of real solutions we have to find the discriminant

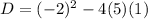
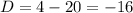
The value of discriminant is -16<0
Hence, the equation has no real roots.
Hence, option 1 is correct