Question

Write the equation of a piecewise function with a jump discontinuity at x =3. Then, determine which step of the 3-step test for continuity that the function

fails.

Answer 1

Here's a possible example:

Explanation:

`f(x) =\begin{cases} x & \quad x < 3\\x+3 & \quad x \geq 3\\\end{cases}`

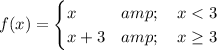
Each piece is linear, so the pieces are continuous by themselves.

We need consider only the point at which the pieces meet (x = 3).

`\displaystyle \lim_(x \longrightarrow 3^(-)) f(x) = \lim_(x \longrightarrow 3^(-)) x = 3\\\\\displaystyle \lim_(x \longrightarrow 3^(+)) f(x) = \lim_(x \longrightarrow 3^(+)) x+3 = 6\\\\f(3) = x + 3 = 6\\\\\displaystyle \lim_(x \longrightarrow 3^(-)) f(x) \\eq f(3)`

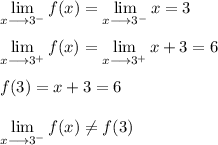
The left-hand limit does not equal ƒ(x), so there is a jump discontinuity at x =3.