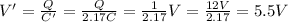Question

A parallel-plate capacitor initially has air (K= 1) between the plates. We first fullycharge it by a 12 V battery. After the battery is disconnected, we insert a dielectricbetween the plates and it completely fills the space in between. A voltmeter is placedacross the capacitor and it reads 3.6 V now.(a) Assuming that there is no charge loss during the process, what is the dielectricconstant of this material?(b) What’s the fraction of the stored energy changed by inserting the dielectric?(c) What will the voltmeter read if the dielectric is pulled partway out so that it fillsonly half of the space in between the plates?

Answer 1

(a) 3.33

For a capacitor with dielectric disconnected from the battery, the relationship between the voltage across the capacitor without the dielectric (V) and with the dielectric (V) is given by

`V' = (V)/(k)`

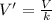
where

k is the dielectric constant of the material

In this problem, we have

`V' = 3.6 V`

`V=12 V`

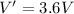
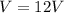
So we can re-arrange the formula to find the dielectric constant:

`k=(V)/(V')=(12 V)/(3.6 V)=3.33`

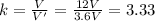
(b) The energy stored reduces by a factor 3.33

The energy stored in a capacitor is

`U=(1)/(2)QV`

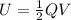
where

Q is the charge stored on the capacitor

V is the voltage across the capacitor

Here we can write the initial energy stored in the capacitor (without dielectric) as

`U=(1)/(2)QV`

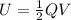
while after inserting the dielectric is

`U'=(1)/(2)QV' = (1)/(2)Q(V)/(k)`

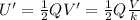
since Q, the charge, has not changed (the capacitor is disconnected, so the charge cannot flow away from the capacitor).

So the ratio between the two energies is

`(U')/(U)=((1)/(2)Q(V)/(k))/((1)/(2)QV)=(1)/(k)`

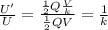
which means

`U' = (U)/(k)=(U)/(3.33)`

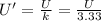
So, the energy stored has decreased by a factor 3.33.

(c) 5.5 V

Pulling the dielectric only partway so that it fills half of the space between the plates is equivalent to a system of 2 capacitors in parallel, each of them with area A/2 (where A is the original area of the plates of the capacitor), of which one of the two is filled with dielectric while the other one is not.

Calling

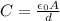`C=(\epsilon_0 A)/(d)` the initial capacitance of the capacitor without dielectric

The capacitance of the part of the capacitor of area A/2 without dielectric is

`C_1 = (\epsilon_0 (A)/(2))/(d)= (C)/(2)`

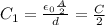
while the capacitance of the part of the capacitor with dielectric is

`C_2 = (k \epsilon_0 (A)/(2))/(d)= (kC)/(2)`

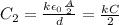
The two are in parallel, so their total capacitance is

`C' = C_1 + C_2 = (C)/(2)+(kC)/(2)=(1+k)(C)/(2)=(1+3.33)(C)/(2)=2.17 C`

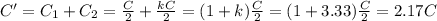
We also have that

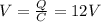`V=(Q)/(C)=12 V` this is the initial voltage

So the final voltage will be

`V' = (Q)/(C')=(Q)/(2.17 C)=(1)/(2.17)V=(12 V)/(2.17)=5.5 V`