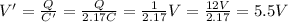(a) 3.33
For a capacitor with dielectric disconnected from the battery, the relationship between the voltage across the capacitor without the dielectric (V) and with the dielectric (V) is given by
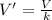
where
k is the dielectric constant of the material
In this problem, we have
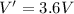

So we can re-arrange the formula to find the dielectric constant:
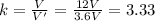
(b) The energy stored reduces by a factor 3.33
The energy stored in a capacitor is

where
Q is the charge stored on the capacitor
V is the voltage across the capacitor
Here we can write the initial energy stored in the capacitor (without dielectric) as

while after inserting the dielectric is
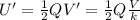
since Q, the charge, has not changed (the capacitor is disconnected, so the charge cannot flow away from the capacitor).
So the ratio between the two energies is
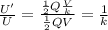
which means
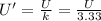
So, the energy stored has decreased by a factor 3.33.
(c) 5.5 V
Pulling the dielectric only partway so that it fills half of the space between the plates is equivalent to a system of 2 capacitors in parallel, each of them with area A/2 (where A is the original area of the plates of the capacitor), of which one of the two is filled with dielectric while the other one is not.
Calling
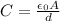 the initial capacitance of the capacitor without dielectric
the initial capacitance of the capacitor without dielectric
The capacitance of the part of the capacitor of area A/2 without dielectric is
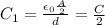
while the capacitance of the part of the capacitor with dielectric is
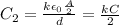
The two are in parallel, so their total capacitance is
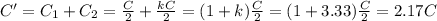
We also have that
 this is the initial voltage
this is the initial voltage
So the final voltage will be