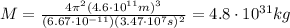(a)
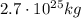
The acceleration due to gravity on the surface of the planet is given by
 (1)
(1)
where
G is the gravitational constant
M is the mass of the planet
R is the radius of the planet
Here we know:
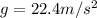
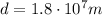 is the diameter, so the radius is
is the diameter, so the radius is
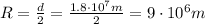
So we can re-arrange eq.(1) to find M, the mass of the planet:
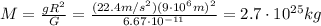
(b)
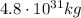
The planet is orbiting the star, so the centripetal force is equal to the gravitational attraction between the planet and the star:
 (1)
(1)
where
m is the mass of the planet
M is the mass of the star
v is the orbital speed of the planet
r is the radius of the orbit
The orbital speed is equal to the ratio between the circumference of the orbit and the period, T:

where
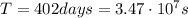
Substituting into (1) and re-arranging the equation
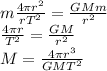
And substituting the numbers, we find the mass of the star: