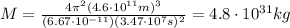Question

You are the science officer on a visit to a distant solar system. Prior to landing on a planet you measure its diameter to be 1.8 × 107 m and its rotation period to be 22.3 hours. You have previously determined that the planet orbits 4.6 × 1011 m from its star with a period of 402 earth days. Once on the surface you find that the acceleration due to gravity is 22.4 m/s2. What are the mass of (a) the planet and (b) the star? (G = 6.67 × 10-11 N · m2/kg2) You are the science officer on a visit to a distant solar system. Prior to landing on a planet you measure its diameter to be 1.8 × 107 m and its rotation period to be 22.3 hours. You have previously determined that the planet orbits 4.6 × 1011 m from its star with a period of 402 earth days. Once on the surface you find that the acceleration due to gravity is 22.4 m/s2. What are the mass of (a) the planet and (b) the star? (G = 6.67 × 10-11 N · m2/kg2) (a) 2.7 × 1025 kg, (b) 2.8 × 1031 kg (a) 5.0 × 1025 kg, (b) 2.8 × 1031 kg (a) 5.0 × 1025 kg, (b) 4.8 × 1031 kg (a) 2.7 × 1025 kg, (b) 4.8 × 1031 kg

Answer 1

(a)
`2.7\cdot 10^(25) kg`

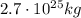
The acceleration due to gravity on the surface of the planet is given by

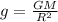`g=(GM)/(R^2)` (1)

where

G is the gravitational constant

M is the mass of the planet

R is the radius of the planet

Here we know:

`g=22.4 m/s^2`

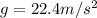
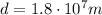`d=1.8\cdot 10^7 m` is the diameter, so the radius is

`R=(d)/(2)=(1.8\cdot 10^7 m)/(2)=9\cdot 10^6 m`

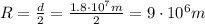
So we can re-arrange eq.(1) to find M, the mass of the planet:

`M=(gR^2)/(G)=((22.4 m/s^2)(9\cdot 10^6 m)^2)/(6.67\cdot 10^(-11))=2.7\cdot 10^(25) kg`

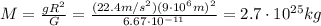
(b)
`4.8\cdot 10^(31)kg`

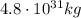
The planet is orbiting the star, so the centripetal force is equal to the gravitational attraction between the planet and the star:

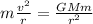`m(v^2)/(r)=(GMm)/(r^2)` (1)

where

m is the mass of the planet

M is the mass of the star

v is the orbital speed of the planet

r is the radius of the orbit

The orbital speed is equal to the ratio between the circumference of the orbit and the period, T:

`v=(2\pi r)/(T)`

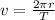
where

`T=402 days = 3.47\cdot 10^7 s`

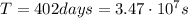
Substituting into (1) and re-arranging the equation

`m(4\pi r^2)/(rT^2)=(GMm)/(r^2)\\(4\pi r)/(T^2)=(GM)/(r^2)\\M=(4\pi r^3)/(GMT^2)`

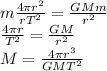
And substituting the numbers, we find the mass of the star:

`M=(4\pi^2 (4.6\cdot 10^(11) m)^3)/((6.67\cdot 10^(-11))(3.47\cdot 10^7 s)^2)=4.8\cdot 10^(31)kg`