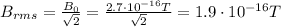Question

During a test, a NATO surveillance radar system, operating at 37 GHz at 182 kW of power, attempts to detect an incoming stealth aircraft at 104 km. Assume that the radar beam is emitted uniformly over a hemisphere. (a) What is the intensity of the beam when the beam reaches the aircraft's location? The aircraft reflects radar waves as though it has a cross-sectional area of only 0.22 m2. (b) What is the power of the aircraft's reflection? Assume that the beam is reflected uniformly over a hemisphere. Back at the radar site, what are (c) the intensity, (d) the maximum value of the electric field vector, and (e) the rms value of the magnetic field of the reflected radar beam?

Answer 1

(a)
`2.68\cdot 10^(-6) W/m^2`

The intensity of an electromagnetic wave is given by

`I=(P)/(A)`

where

P is the power

A is the area of the surface considered

For the waves in the problem,

`P=182 kW = 1.82\cdot 10^5 W` is the power

The area is a hemisphere of radius

`r=104 km=1.04\cdot 10^5 m`

so

`A=2\pi r^2=2\pi (1.04\cdot 10^5 m)^2=6.8\cdot 10^(10) m^2`

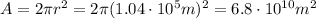
So, the intensity is

`I=(1.82\cdot 10^5 W)/(6.8\cdot 10^(10)m^2)=2.68\cdot 10^(-6) W/m^2`

(b)
`5.9\cdot 10^(-7) W`

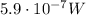
In this case, the area of the reflection is

`A=0.22 m^2`

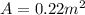
So, if we use the intensity of the wave that we found previously, we can calculate the power of the aircraft's reflection using the same formula:

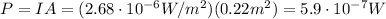
`P=IA=(2.68\cdot 10^(-6) W/m^2)(0.22 m^2)=5.9\cdot 10^(-7) W`

(c)
`8.7\cdot 10^(-18) W/m^2`

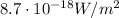
We said that the power of the waves reflected by the aircraft is

`P=5.9\cdot 10^(-7) W`

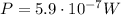
If we assume that the reflected waves also propagate over a hemisphere of radius

`r=104 km=1.04\cdot 10^5 m`

which has an area of

`A=2\pi r^2=2\pi (1.04\cdot 10^5 m)^2=6.8\cdot 10^(10) m^2`

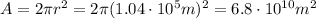
Then the intensity of the reflected waves at the radar site will be

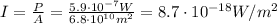
`I=(P)/(A)=(5.9\cdot 10^(-7) W)/(6.8\cdot 10^(10) m^2)=8.7\cdot 10^(-18) W/m^2`

(d)
`8.1\cdot 10^(-8) V/m`

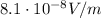
The intensity of a wave is related to the maximum value of the electric field by

`I=(1)/(2)c\epsilon_0 E_0^2`

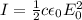
where

c is the speed of light

`\epsilon_0` is the vacuum permittivity

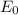`E_0` is the maximum value of the electric field vector

Solving the equation for
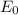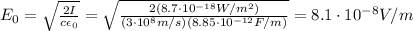
`E_0`,

`E_0=\sqrt{(2I)/(c\epsilon_0)}=\sqrt{(2(8.7\cdot 10^(-18) W/m^2))/((3\cdot 10^8 m/s)(8.85\cdot 10^(-12) F/m))}=8.1\cdot 10^(-8) V/m`

(e)
`1.9\cdot 10^(-16) T`

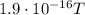
The maximum value of the magnetic field vector is given by

`B_0 = (E_0)/(c)`

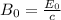
Substituting the values,

`B_0 = ((8.1\cdot 10^(-8) V/m))/(3\cdot 10^8 m/s)=2.7\cdot 10^(-16) T`

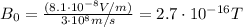
And the rms value of the magnetic field is given by

`B_(rms) = (B_0)/(√(2))=(2.7\cdot 10^(-16) T)/(√(2))=1.9\cdot 10^(-16) T`