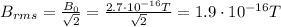(a)
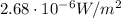
The intensity of an electromagnetic wave is given by
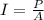
where
P is the power
A is the area of the surface considered
For the waves in the problem,
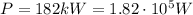 is the power
is the power
The area is a hemisphere of radius
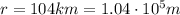
so
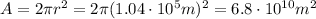
So, the intensity is
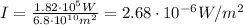
(b)
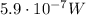
In this case, the area of the reflection is
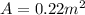
So, if we use the intensity of the wave that we found previously, we can calculate the power of the aircraft's reflection using the same formula:
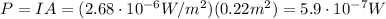
(c)
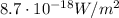
We said that the power of the waves reflected by the aircraft is
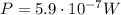
If we assume that the reflected waves also propagate over a hemisphere of radius
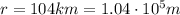
which has an area of
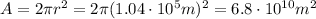
Then the intensity of the reflected waves at the radar site will be
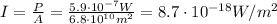
(d)
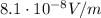
The intensity of a wave is related to the maximum value of the electric field by
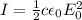
where
c is the speed of light
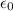 is the vacuum permittivity
is the vacuum permittivity
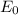 is the maximum value of the electric field vector
is the maximum value of the electric field vector
Solving the equation for
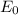 ,
,
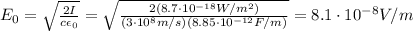
(e)
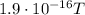
The maximum value of the magnetic field vector is given by
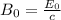
Substituting the values,
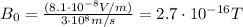
And the rms value of the magnetic field is given by