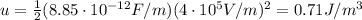Question

A 2.0-cm-diameter parallel-plate capacitor with a spacing of 0.50 mm is charged to 200 V?What is the total energy stores in the electic field?U=______ JWhat is the energy densityu=________J/m^3

Answer 1

1)
`1.11\cdot 10^(-7) J`

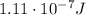
The capacitance of a parallel-plate capacitor is given by:

`C=(\epsilon_0 A)/(d)`

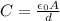
where

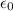`\epsilon_0` is the vacuum permittivity

A is the area of each plate

d is the distance between the plates

Here, the radius of each plate is

`r=(2.0 cm)/(2)=1.0 cm=0.01 m`

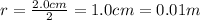
so the area is

`A=\pi r^2 = \pi (0.01 m)^2=3.14\cdot 10^(-4) m^2`

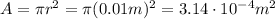
While the separation between the plates is

`d=0.50 mm=5\cdot 10^(-4) m`

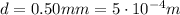
So the capacitance is

`C=((8.85\cdot 10^(-12) F/m)(3.14\cdot 10^(-4) m^2))/(5\cdot 10^(-4) m)=5.56\cdot 10^(-12) F`

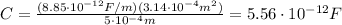
And now we can find the energy stored,which is given by:

`U=(1)/(2)CV^2=(1)/(2)(5.56\cdot 10^(-12) F/m)(200 V)^2=1.11\cdot 10^(-7) J`

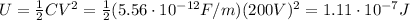
2) 0.71 J/m^3

The magnitude of the electric field is given by

`E=(V)/(d)=(200 V)/(5\cdot 10^(-4) m)=4\cdot 10^5 V/m`

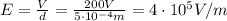
and the energy density of the electric field is given by

`u=(1)/(2)\epsilon_0 E^2`

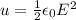
and using

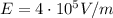`E=4\cdot 10^5 V/m`, we find

`u=(1)/(2)(8.85\cdot 10^(-12) F/m)(4\cdot 10^5 V/m)^2=0.71 J/m^3`