1)
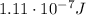
The capacitance of a parallel-plate capacitor is given by:
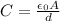
where
 is the vacuum permittivity
is the vacuum permittivity
A is the area of each plate
d is the distance between the plates
Here, the radius of each plate is
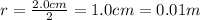
so the area is

While the separation between the plates is

So the capacitance is
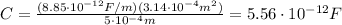
And now we can find the energy stored,which is given by:
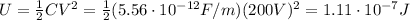
2) 0.71 J/m^3
The magnitude of the electric field is given by

and the energy density of the electric field is given by

and using
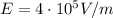 , we find
, we find
