Question

The volume in cubic feet of a box can be expressed as (x) = x^3 - 6x^2 + 8x , or as the product of three linear factors with integer coefficients. The width of the box is x-2. Factor the polynomial to find linear expressions for the height and the length. Show your work.

Answer 1

Either the height is
`x` and the length is
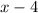`x-4` or the other way round.

Explanation:

The volume is given in terms of x as
`V(x)=x^3-6x^2+8x`.

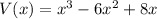We factor the GCF to get;

`V(x)=x(x^2-6x+8)`.

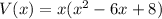We split the middle term of the trinomial in the parenthesis.

`V(x)=x(x^2-4x-2x+8)`.

We now factor the expression within the parenthesis by grouping;

`V(x)=x[x(x-4)-2(x-4)]`.

`V(x)=x(x-2)(x-4)`.

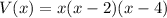Since the width of the box is
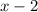`x-2` units, the linear expression for the height and length is
`x(x-4)`

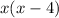
Either the height is
`x` and the length is
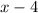`x-4` or the other way round.