Answer:
Either the height is
 and the length is
and the length is
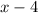 or the other way round.
or the other way round.
Explanation:
The volume is given in terms of x as
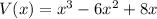 .
.
We factor the GCF to get;
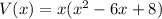 .
.
We split the middle term of the trinomial in the parenthesis.
 .
.
We now factor the expression within the parenthesis by grouping;
![V(x)=x[x(x-4)-2(x-4)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/c96j6cz01f5yudfkfkrnbev4kbnva78byu.png) .
.
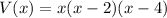 .
.
Since the width of the box is
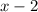 units, the linear expression for the height and length is
units, the linear expression for the height and length is
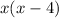
Either the height is
 and the length is
and the length is
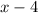 or the other way round.
or the other way round.