Answer:
10.
![\sqrt[]{x^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9zzty9s3bhkwnvjqn3mhgz5g3m94tnjvp0.png)
11.
![\sqrt[3]{x^5}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mpis8zj2k7vwoisa5qu57xcz90homggomb.png)
12.
a. the sum of 2 rational numbers: is always a rational number. (ex: 2 + 2 = 4)
b. the sum of an irrational and a rational number: is not rational (ex: 1/3 + π)
c. the product of 2 rational numbers: is a rational number (ex: 45/2 × 4/7 = 90/7)
d. the product of an irrational and a rational number: not rational (ex: 4/5 × π)
Explanation:
10. to write an exponent in radical form, we can use the following formula:
![a^(z)/(n) = \sqrt[n]{a^z}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5k1o0hf4xko6flc26lvr3ybdub2uecrge6.png)
looking at
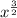 , we can convert it to a radical using the formula, in which x = a, z = 3 and n = 2, we have the following:
, we can convert it to a radical using the formula, in which x = a, z = 3 and n = 2, we have the following:
![\sqrt[]{x^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9zzty9s3bhkwnvjqn3mhgz5g3m94tnjvp0.png) < we did not write 2 because 2 is the square root symbol with no need to write a 2
< we did not write 2 because 2 is the square root symbol with no need to write a 2
11. using the same formula as above, we can convert the radical into exponential form
in
![\sqrt[3]{x^5}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mpis8zj2k7vwoisa5qu57xcz90homggomb.png) , our values are: a = x, z = 5 and n = 3. we can write it as:
, our values are: a = x, z = 5 and n = 3. we can write it as:
![\sqrt[3]{x^5}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mpis8zj2k7vwoisa5qu57xcz90homggomb.png)
12.
a. the sum of 2 rational numbers: is always a rational number. (ex: 2 + 2 = 4)
b. the sum of an irrational and a rational number: is not rational (ex: 1/3 + π)
c. the product of 2 rational numbers: is a rational number (ex: 45/2 × 4/7 = 90/7)
d. the product of an irrational and a rational number: not rational (ex: 4/5 × π)