Question

I need some help with this, Thanks

Answer 1

10.
`\sqrt[]{x^3}`

11.
`\sqrt[3]{x^5}`

12.

a. the sum of 2 rational numbers: is always a rational number. (ex: 2 + 2 = 4)

b. the sum of an irrational and a rational number: is not rational (ex: 1/3 + π)

c. the product of 2 rational numbers: is a rational number (ex: 45/2 × 4/7 = 90/7)

d. the product of an irrational and a rational number: not rational (ex: 4/5 × π)

Explanation:

10. to write an exponent in radical form, we can use the following formula:

`a^(z)/(n) = \sqrt[n]{a^z}`

looking at
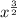`x^(3)/(2)`, we can convert it to a radical using the formula, in which x = a, z = 3 and n = 2, we have the following:

`\sqrt[]{x^3}` < we did not write 2 because 2 is the square root symbol with no need to write a 2

11. using the same formula as above, we can convert the radical into exponential form

in
`\sqrt[3]{x^5}`, our values are: a = x, z = 5 and n = 3. we can write it as:

`\sqrt[3]{x^5}`

12.

a. the sum of 2 rational numbers: is always a rational number. (ex: 2 + 2 = 4)

b. the sum of an irrational and a rational number: is not rational (ex: 1/3 + π)

c. the product of 2 rational numbers: is a rational number (ex: 45/2 × 4/7 = 90/7)

d. the product of an irrational and a rational number: not rational (ex: 4/5 × π)