Question

The hypotenuse of a right angle triangle measures 12 units. what is the maximum possible area in square units, of the triangle ?

Answer 1

The maximum possible area of the triangle is 36 units²

Explanation:

Let

x, y the legs of the right triangle

Applying the Pythagoras Theorem

`12^(2)=x^(2)+y^(2)\\\\144=x^(2)+y^(2)`

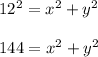
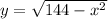`y=\sqrt{144-x^(2)}` ----> equation A

The area of the right triangle is equal to

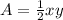`A=(1)/(2)xy` ----> equation B

substitute equation A in equation B

`A=(1)/(2)x(\sqrt{144-x^(2)})`

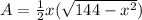
Using a graphing tool

The vertex of the graph is a maximum

That means

The x-coordinate of the vertex is the value of x for the maximum possible area of the triangle

The y-coordinate of the vertex is the maximum possible area of the triangle

The vertex is the point (8.485,36)

see the attached figure

therefore

The maximum possible area of the triangle is 36 units²