Answer:

Explanation:
The three step test for continuity states that a function ƒ(x) is continuous at a point x = a if three conditions are satisfied:
- f(a) is defined.
- The limit of ƒ(x) as x approaches a exists.
- The limit of ƒ(x) as x approaches a is equal to f(a).
(i) Left-hand limit = right-hand limit.
Pass. The limit from either side is 8.
(ii) Left-hand limit = limit.
Pass. If the limits from either direction exist, the limit exists.
(iii) Limit as x ⟶ ∞ is not part of the three-step test.
(iv) Limit as x ⟶ 1 exists. Pass.
(v) f(1) is defined.
FAIL. f(1) is not defined.
(vi) Limit as x ⟶ ∞ is not part of the three-step test.
(vii) Passing the three-step test is not a step in the test.
(viii) The limit as x ⟶ 1 does not equal f(1).
FAIL. f(1) is undefined.
The steps in the three-step test for which the function fails are
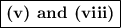 .
.