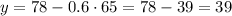Answer:
65 ft by 39 ft
Explanation:
Let x ft be the length of each part and y ft be the width of each part. The total perimeter of all 5 parts is
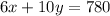
The length of the large rectangle is 5y ft and the width of the large rectangle is x, so the total area is
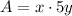
From the first equation,
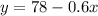
Substitute it into the area expression:
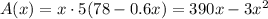
Find the derivative:
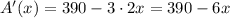
Equate it to 0:
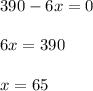
Then